ECUACIONES
¿Qué
es una ecuación?
Una
ecuación en matemática se define como una igualdad establecida entre dos
expresiones, en la cual puede haber una o más incógnitas que deben ser
resueltas.
Las
ecuaciones sirven para resolver diferentes problemas matemáticos, geométricos,
químicos, físicos o de cualquier otra índole, que tienen aplicaciones tanto en
la vida cotidiana como en la investigación y desarrollo de proyectos
científicos.
Las
ecuaciones pueden tener una o más incógnitas, y también puede darse el caso de
que no tengan ninguna solución o de que sea posible más de una solución.
Partes
de una ecuación
Las
ecuaciones están formadas por diferentes elementos. Veamos cada uno de ellos.
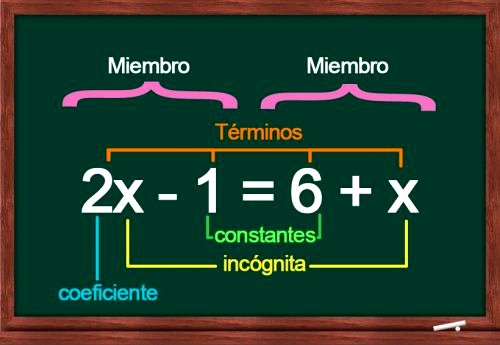
Cada
ecuación tiene dos miembros, y estos se separan mediante el uso del signo igual
(=).
Cada
miembro está conformado por términos, que corresponden a cada uno de los
monomios.
Los
valores de cada monomio de la ecuación pueden ser de diferente tenor. Por
ejemplo:
constantes;
coeficientes;
variables;
funciones;
vectores.
Las
incógnitas, es decir, los valores que se desean encontrar, se representan con
letras. Veamos un ejemplo de ecuación.
Tipos
de ecuaciones
Existen
diferentes tipos de ecuaciones de acuerdo a su función. Conozcamos cuáles son.
1.
Ecuaciones algebraicas
Las
ecuaciones algebraicas, que son las fundamentales, se clasifican o subdividen
en los diversos tipos que se decriben a continuación.
a.
Ecuaciones de primer grado o ecuaciones lineales
Son
las que involucran una o más variables a la primera potencia y no presenta
producto entre variables.
Por
ejemplo: a x + b = 0
Vea
también: Ecuación de primer grado
b.
Ecuaciones de segundo grado o ecuaciones cuadráticas
En
este tipo de ecuaciones, el término desconocido está elevado al cuadrado.
Por
ejemplo: ax2 + bx + c = 0
c.
Ecuaciones de tercer grado o ecuaciones cúbicas
En
este tipo de ecuaciones, el término desconocido está elevado al cubo.
Por
ejemplo: ax3+ bx2 + cx + d = 0
d.
Ecuaciones de cuarto grado
Aquellas
en las que a, b, c y d son números que forman parte de un cuerpo que puede ser ℝ o a ℂ.
Por
ejemplo: ax4 + bx3 + cx2 + dx + e = 0
2.
Ecuaciones trascendentes
Son un tipo de ecuación que no se puede resolver solo mediante operaciones algebraicas, es decir, cuando incluye al menos una función no algebraica.
Por
ejemplo,
ecuacion
3.
Ecuaciones funcionales
Son aquellas cuya incógnita son una función de una variable.
Por ejemplo,
ecuacion
4. Ecuaciones integrales
Aquella
en que la función incógnita se encuentra en el integrando.
ecuacion
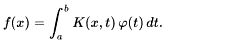
5.
Ecuaciones diferenciales
Aquellas
que ponen en relación una función con sus derivadas.
ecuacion
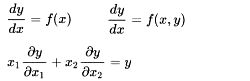
No hay comentarios.:
Publicar un comentario