GEOMETRÍA
PLANA
La geometría plana es una rama de
geometría dedicada al estudio de las figuras bidimensionales, es decir,
aquellas que se grafican en un plano.
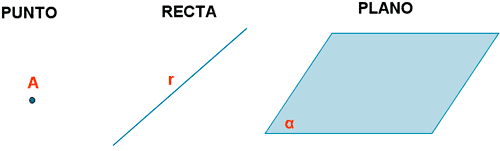
La geometría plana analiza elementos
como unidimensionales como la recta, la semirrecta y el segmento. De igual
modo, forman parte de este campo de estudios los ángulos y los polígonos.
Esta rama de geometría implica
muchas veces la simplificación del mundo que nos rodea en un plano, de manera
que no pueden estudiarse todas las características de los objetos. Por ejemplo,
no se podría analizar todas las dimensiones de una caja, sino cada una de sus
caras que son cuadriláteros.
La geometría plana tiene sus orígenes en la antigüedad, siendo su principal antecedente la obra Los Elementos del matemático griego Euclides y que data del siglo IV A.C. Este es considerado como uno de los textos más influyentes de la historia y recopila nociones básicas de elementos como rectas y polígonos, e incluso podemos encontrar el famoso teorema de Pitágoras.
Los
elementos que estudia la geometría plana son:
Recta:
Es un elemento unidimensional constituido por una serie infinita de puntos que
van a una sola dirección, es decir, no presenta curvas.
Semirrecta:
Al igual que la recta, es un elemento unidimensional que consiste en una
secuencia de puntos, pero no es indefinida, sino que tiene un origen y se
prolonga al infinito. Puede definirse también como la porción de una recta
definida a partir de un punto de corte.
Segmento:
Es un elemento unidimensional constituido puntos que van en una sola dirección,
pero , a diferencia de la semirrecta, está acotado por un punto de origen y un
final.
Ángulo:
Es el arco que se forma a partir del cruce u origen de dos elementos
bidimensionales, ya sean rectas, semirrectas o segmentos.
Polígono:
Es una figura bidimensional formada por una serie finita de segmentos no
colineales (no forman parte de la misma recta), de manera que forman un espacio
cerrados. Algunos ejemplos son los cuadrados, los rectángulos, los rombos, los
triángulos o los octógonos. Los polígonos pueden clasificarse en:
Regulares:
Cuando todos sus lados y ángulos interiores tienen la misma medida.
Irregulares:
Cuando no todos sus lados y ángulos interiores son idénticos.
Circunferencia:
Es una figura geométrica plana y cerrada que se caracteriza porque todos los
puntos que la constituyen se ubican a la misma distancia del centro. Dicha
distancia constante se llama radio. También se define a la circunferencia como
el perímetro del círculo.
Polígonos
Un
polígono es una figura plana cerrada que está formada por tres o más segmentos
de recta que se unen en sus puntos extremos. Los segmentos de recta que forman
un polígono solo se intersectan en sus puntos extremos. Los polígonos se
nombran de acuerdo al número de lados que están formados.
Triángulo:
polígono de 3 lados
Cuádrilatero:
polígono de 4 lados
Pentagono:
polígono de 5 lados
Hexágono:
polígono de 6 lados
Heptágono:
polígono de 7 lados
Octágono:
polígono de 8 lados
Nonágono:
polígono de 9 lados
Decágono:
polígono de 10 lados
Dodecágono:
polígono de 12 lados
n -
ágono: polígono de n lados
Las partes de un polígono son:
Vértices:
puntos finales de los segmentos que forma el polígono, en la figura: A, B, C,
D, E.
Lados:
segmentos de recta que unen dos vértices consecutivos del polígono, en la
figura los lados son: AB,
Lados
consecutivos: cualquier par de lados que comparten un vértice, en la figura: AB
y BC, BC y CD,
Diagonal:
un segmento de recta que une dos vértices no consecutivos, en la figura: AC.
Apotema:
de un polígono regular es la menor distancia entre el centro y cualquiera de
sus lados. Es un segmento cuyos extremos son el centro de un polígono regular y
el punto medio de uno cualquiera de sus lados, y es siempre perpendicular a
dicho lado.
Círculos
El
círculo es una figura plana que consiste de todos los puntos que están sobre
una curva cerrada y de los puntos interiores de ella, en la cual cada punto sobre
la curva tiene la misma distancia al centro del círculo.
El
radio de un círculo es la distancia entre el centro y cualquier punto de la
curva y tiene longitud r.
El
diámetro de un círculo es la distancia entre dos puntos cualesquiera de la
curva cerrada y que pasa por el centro y tiene longitud d = 2r y divide a un
círculo en dos partes iguales.
La
Circunferencia es la línea curva cerrada y plana cuyos puntos están a la misma
distancia (radio) de un punto (centro). El centro no es parte de la
circunferencia.
El
área de un círculo, es la medida de la superficie limitada por la
circunferencia del círculo dado.
En la
siguiente aplicación mueve los deslizadores y luego:
Compara
las superficies del polígono inscrito en la circunferencia y la del círculo
delimitado por la misma.
Aumenta
el número de lados y cambia la longitud del radio ¿Qué harías para que la
superficie del polígono fuese lo más parecida posible a la del círculo?
Activa
las casillas "Datos del polígono" y "Radio". Repite las
actividades uno y dos. Comprueba que la respuesta que has dado en la actividad
dos es la correcta.
Activa
las casillas "Área del polígono" y "Área del círculo".
Comprueba si la respuesta dada en la actividad dos es acorde con los datos de
las





No hay comentarios.:
Publicar un comentario